Last Updated: Monday, February 4, 2013
The most remarkable feature of the glenohumeral joint is its ability to precisely stabilize the humeral head in the center of the glenoid on one hand and to allow a vast range of motion on the other. This balance of stability and mobility is achieved by a combination of mechanisms particular to this articulation.
About the glenohumeral joint
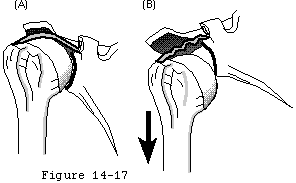
In contrast to the hip joint the glenohumeral joint does not offer a deep stabilizing socket. An acetabular-like socket would limit motion by contact of the anatomic neck of the humerus with its rim. Instead the small arc of the glenoid captures relatively little of the humeral articular surface so that neck-rim contact is avoided for a wide range of positions (see figure 1). (Das 1966; Maki and Gruen 1976; Matsen et al 1994; Saha 1971; Turkel et al. 1981)
In contrast to hinge-like joints with shallow sockets such as the knee interphalangeal joints elbow and ankle the glenohumeral joint does not offer isometric articular ligaments which provide stability as the joint is flexed around a defined anatomical axis. Instead the glenohumeral ligaments play important stabilizing roles only at the extremes of motion being lax and relatively ineffectual in most functional positions of the joint (see figure 2). (Matsen et al 1994; Warner et al 1992)
In spite of its lack of a deep socket or isometric ligaments the normal shoulder precisely constrains the humeral head to the center of the glenoid cavity throughout most of the arc of movement. (Howell and Galinat 1989; Howell et al 1988; Poppen and Walker 1976; Poppen and Walker 1978). It is remarkable that this seemingly unconstrained joint is able to provide this precise centering resist the gravitational pull on the arm hanging at the side for long periods remain located during sleep allow for the lifting of large loads permit throwing a baseball at speeds approaching 100 miles an hour and maintain stability during the application of an almost infinite variety of forces of differing magnitude direction duration and abruptness.
The mechanics of glenohumeral stability can be most easily understood in terms of the relationship between the net force acting on the humeral head and the shape of the glenoid fossa. A working familiarity with the mechanics of glenohumeral stability will greatly enhance understanding of the workings of the normal joint laboratory models of instability clinical problems of instability and clinical strategies for managing glenohumeral instability.
Basic laws
The basic laws of glenohumeral stability can be stated as follows:
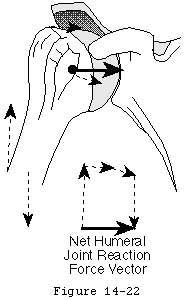
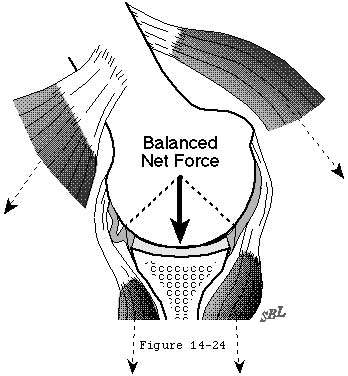
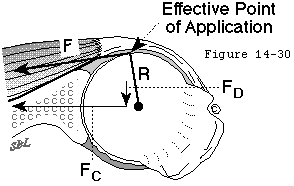
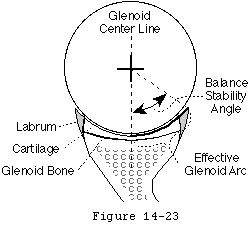
- the glenohumeral joint will not dislocate as long as the net humeral joint reaction force (footnote 1) (see figure 3) is directed within the effective glenoid arc (footnote 2) (see figures 4 and 5).
- the humeral head will remained centered in the glenoid fossa if the glenoid and humeral joint surfaces are congruent and if the net humeral joint reaction force is directed within the effective glenoid arc.
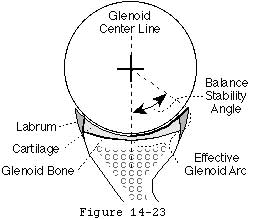
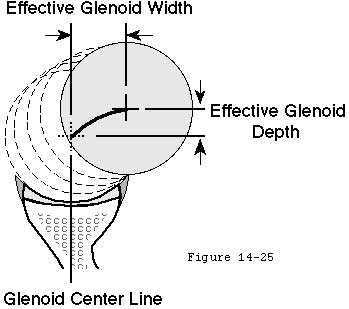
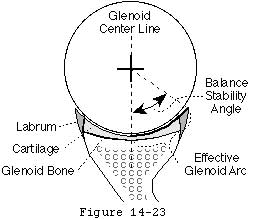
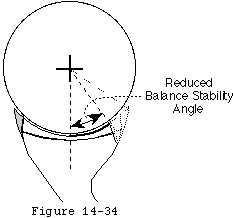
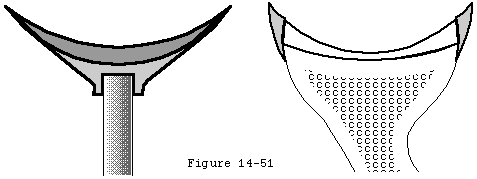
The effective shape of the glenoid is revealed by the glenoidogram which rather than showing how the glenoid looks shows how it works (see figures 6 and 7). (Lazarus et al 1996; Matsen et al 1994) The glenoidogram is the path taken by the center of the humeral head as it is translated away from the center of the glenoid fossa in a specified direction under defined loads. The shape of the glenoidogram indicates the extent of the effective glenoid arc in that direction. If the net humeral joint reaction force passes outside the effective glenoid arc the joint becomes unstable. The glenoidogram is oriented with respect to the glenoid center line a reference line perpendicular to the center of the glenoid fossa (see figures 8 and 9). The maximal angle that the net humeral joint reaction force can make with the glenoid center line in a given direction is the balance stability angle (see figures 10 and 11). The balance stability angles vary for different directions around the glenoid. The requisite for a stable glenohumeral joint is that the net humeral joint reaction force is maintained within the balance stability angles.
Footnotes
Footnote 1: The "net humeral joint reaction force" is the resultant of all muscular ligamentous inertial gravitational and other external forces applied to the head of the humeral head (other than the force applied by the glenoid).
Footnote 2: Recognizing that the rim of the glenoid is deformable under load the "effective glenoid arc" is the arc of the glenoid available to support the humeral head under the specified loading conditions.
Click to enlarge
Figure 11
The direction of the net humeral joint reaction force is controlled actively by the elements of the rotator cuff and other shoulder muscles.
Neuromuscular training
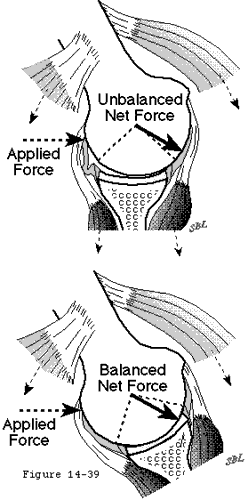
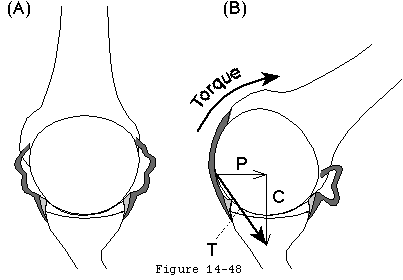
Each active muscle generates a force whose direction is determined by the effective origin and insertion of that muscle (see figure 12). The neural control of the magnitude of these muscle forces provides the mechanism by which the direction of the net humeral joint reaction force is controlled. For example by increasing the force of contraction of a muscle whose force direction is close to the glenoid center line the direction of the net humeral joint reaction force can be aligned more closely with the glenoid fossa (see figure 13).
The elements of the rotator cuff are well positioned to contribute to this muscle balance. (Basmajian and DeLuca 1985; Bassett et al 1990; Blasier et al 1992; Cain et al 1987; Harryman et al 1996 Itoi et al 1993; Itoi et al 1994; Karlsson and Peterson 1992; Pagnani et al 1995; Perry and Glousman 1989; Rodosky et al 1994; Sarrafian 1983; Van der Helm 1994; Van der Helm et al 1992; Veeger et al. 1991; Wulker et al 1995)
Strengthening and neuromuscular training help optimize the neuromuscular control of the net humeral joint reaction force. Conversely the net humeral joint reaction force is difficult to optimize when muscle control is impaired by injury disuse contracture paralysis loss of coordination or tendon defects (see figure 14).
Neuromuscular training may be guided by proprioceptors in the labrum and ligaments (Guanche et al 1995; Hashimoto et al 1994; Jerosch et al 1995; Vangsness et al 1995) which may help guide neuromuscular training. Blasier et al (Blasier et al 1994) and Kronberg et al (Kronberget al 1991) showed that individuals with generalized joint laxity have less acute proprioception and altered muscle activation. Zuckerman et al demonstrated that motion and position sense are compromised in the presence of traumatic anterior instability and restored at one year after surgical reconstruction. (Zuckerman et al. 1996)
The balance stability angle is the maximal angle that the net humeral joint reaction force can make with the glenoid center line before glenohumeral dislocation occurs. The tangent of this balance stability angle is the ratio between its displacing component (perpendicular to the glenoid center line) and its compressive component (parallel to the glenoid center line) which is known as the stability ratio.
Displacing forces
The stability ratio is the maximal displacing force in a given direction that can be stabilized by specified compressive load assuming frictional effects to be minimal (footnote 1). The effective glenoid arc the balance stability angle and stability ratios vary around the perimeter of the glenoid (see figure 15). It is handy to note that for small angles the stability ratio can be estimated by dividing the balance stability angle by 57 degrees (footnote 2).
Stability ratio
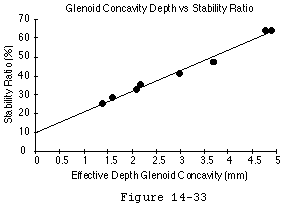
The stability ratio is frequently used in the laboratory because it is relatively easy to measure: a compressive load is applied and the displacing force is progressively increased until dislocation occurs. For example Lippitt et al (Lippitt et al 1993) found that a compressive load of 50N resisted displacing loads up to 30N and that the effectiveness of this stabilization mechanism varied with the depth of the glenoid.
Investigation of these parameters provides important information on stability mechanics for example resection of the labrum has been shown to reduce the stability ratio by 20 per cent. (Lippitt Vanderhooft Harris et al 1993) Furthermore a three millimeter anterior glenoid defect has been shown to reduce the balance stability angle over 25 per cent from 18 to 13 degrees. (Matsen Lippitt Sidles et al 1994)
Clinically the stability ratio can be sensed using the "load and shift" test wherein the examiner applies a compressive load pressing the humeral head into the glenoid while noting the amount of translating force necessary to move the humeral head from its centered position. (Silliman and Hawkins 1993) This test gives the examiner an indication of the adequacy of the glenoid concavity and is one of the most practical ways to detect deficiencies of the glenoid rim.
Footnotes
Footnote 1: Measured stability ratios may be influenced by the friction of the joint surfaces and by other stabilizing mechanisms such as adhesion/cohesion and the glenoid suction cup (which will be discussed later). These effects will tend to increase the displacing force necessary to dislocate the humeral head for a given compressive load. It is essential to control for these effects in the laboratory. Specifically the under-lubricated aged cadaver joints available to the lab may have substantially greater coefficients of friction in vitro than the exquisitely lubricated and smooth joint of the young person in vivo.
Footnote 2: At small angles the tangent of an angle is approximately equal to the angle expressed in radians. Thus the stability ratio (tangent of the balance stability angle) is approximately the balance stability angle divided by 57 degrees per radian.
Effective shape of the glenoid
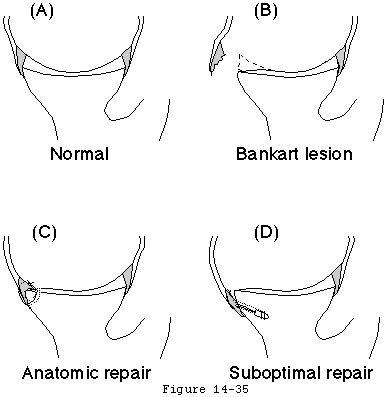
The glenoid concavity is formed by a combination of the shape of the underlying bone and the overlying cartilage and labrum (see figures 17 and 18). (Howell and Galinat 1989; Soslowsky et al 1992) The effective glenoid arc may be compromised by congenital deficiency (glenoid hypoplasia) excessive compliance traumatic lesions (rim fractures or Bankart defects) or wear (see figure 19). (Altchek et al 1991; Baker et al 1990; Bankart 1938; Cooper and Brems 1992; Cyprien et al 1983; Howell and Galinat 1989; Joessel 1880; Lazarus Sidles Harryman et al 1996; Lippitt Vanderhooft Harris et al 1993; Matsen Lippitt Sidles et al 1994; Matsen and Thomas 1990 Matsen et al 1990; Neer and Foster 1980; Pappas et al 1983; Rowe Patel and Southmayd 1978; Thomas and Matsen 1989) The effective arc may be augmented by anatomical repair of fractures or Bankart lesions (see figure 20) by rim augmentation by congruent glenoid bone grafting and by glenoid osteotomy. (Lazarus Sidles Harryman et al 1996)
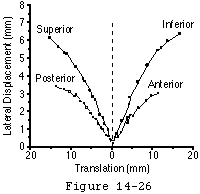
The effective shape of the glenoid is revealed by the glenoidogram. As the humeral head is translated from the center of the glenoid to the rim in a given direction the center of the humeral head traces the glenoidogram which has a characteristic gull-wing shape. The glenoidogram is different for different directions of translation as shown in (see figure 21) which demonstrates data recorded for the superior inferior anterior and posterior directions in a typical shoulder. The shape of the glenoidogram can be predicted from the humeral radius of curvature the glenoid radius of curvature and the balance stability angle (footnote 1).
Glenoidograms
Predicted glenoidograms are qualitatively similar to glenoidograms measured experimentally (see figure 5). The glenoidogram also reveals another important aspect of shoulder stability: the slope of the glenoidogram at any point is equal to the tangent of the balance stability angle (which equals the stability ratio) at that point. For most glenoidograms it can be seen that the slope is steepest when the humeral head is centered in the glenoid. Thus the joint has the highly desirable property of being most stable when the head is centered. As the humeral head is moved away from the center the slope of the glenoidogram and the stability ratio become less.
Thus as the head is displaced from the glenoid center it becomes progressively more unstable. Once enough force is applied to displace the head from the center that same amount of force would easily displace the humeral head over the glenoid lip. Note also that when the humeral head is translated to the lip of the glenoid the stability ratio is as expected zero. These observations relate to the "jerk" tests described for anterior (Lerat et al 1994) and posterior (Matsen Lippitt Sidles et al 1994) instability: in these tests there is no translation of the humeral head until the point where sudden and substantial translation occurs. (Lazarus Sidles Harryman et al 1996; Lippitt Vanderhooft Harris et al 1993)
Footnotes
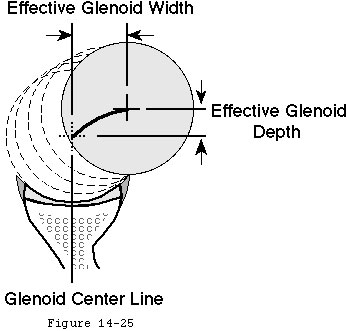
Footnote 1: Glenoidograms can be predicted given the radius of curvature of the humeral head (Rh) the radius of curvature of the glenoid fossa (Rg) the effective glenoid width (W) and the effective glenoid depth (D) and the balance stability angle (BSA) in radians. For each value of x (the distance away from the glenoid center line) the perpendicular distance of the center of the humeral head away from the glenoid bottom y is given by D - Rh + SQRT(RhRh-(W-x)(W-x)). The sample spreadsheet displays the case where Rg = Rh = 25 mm and the BSA = 30° = 0.5236 radians. In this case the effective glenoid width (W) is = RgSin(BSA) and the effective glenoid depth (D) is = Rg(1-Cos(BSA)). The results of this prediction are shown in Table 1.
Table 1
| Effective glenoid Width | Effective Glenoid Depth | ||
| W | D | x | y |
| Rg*Sin(BSA) | Rg*(1-Cos(BSA)) | D-Rh+SQRT(RhRh-(W-x)(W-x)) | |
| 12.50 | 3.35 | 0 | 0 |
| 12.50 | 3.35 | 0.1 | 0.057428086 |
| 12.50 | 3.35 | 0.2 | 0.114245197 |
| 12.50 | 3.35 | 0.3 | 0.170456105 |
| 12.50 | 3.35 | 0.4 | 0.226065482 |
| 12.50 | 3.35 | 0.5 | 0.281077905 |
| 12.50 | 3.35 | 0.6 | 0.335497855 |
| 12.50 | 3.35 | 0.7 | 0.38932972 |
| 12.50 | 3.35 | 0.8 | 0.442577799 |
| 12.50 | 3.35 | 0.9 | 0.495246303 |
| 12.50 | 3.35 | 1 | 0.547339357 |
About the version
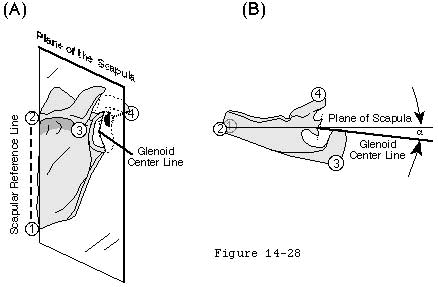
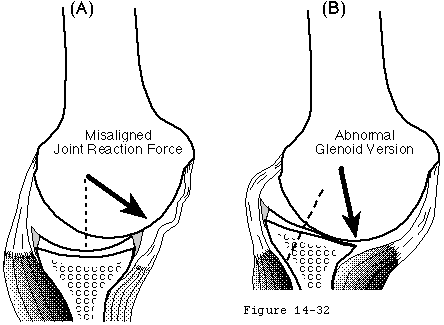
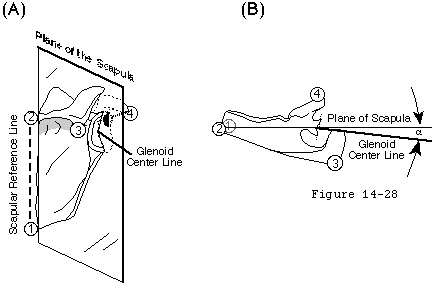
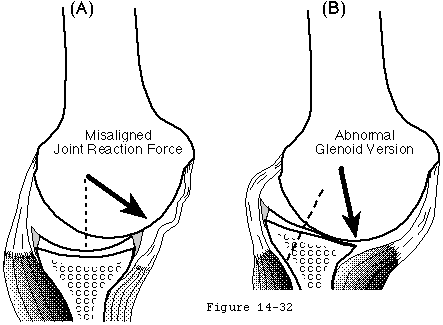
Glenoid version is the angle that the glenoid center line makes with the plane of the scapula (see figure 22). The glenoid center line usually points a few degrees posterior to the plane of the scapula (see figure 22). Changing the version of the glenoid articular surface imposes a corresponding change in the humeroscapular positions in which the net humeral joint reaction force will be contained by the effective glenoid arc. Glenoid version may be altered by glenoid dysplasia (see figure 23) (Wirth et al 1993) fractures glenoid osteotomy (Wirth et al 1994) and glenoid arthroplasty. Abnormal glenoid version positions the glenoid fossa in an abnormal relationship to the forces generated by the scapulohumeral muscles. Normalizing abnormal glenoid version is often a critical step in glenohumeral reconstruction.
Apparent changes in glenoid version can arise from loss of part of the glenoid rim (see figures 24 and 25). (Breweret al 1986; Hurley et al 1992; Randelli and Gambrioli 1986) Dias et al found no difference in apparent glenoid version between normal subjects and recurrent anterior dislocators. (Dias et al 1993) Dowdy and O'Driscoll (Dowdy and O'Driscoll 1994) found only minor variances of radiographic glenoid version among patients with and without recurrence following stabilization surgery. However Hirschfelder and Kirsten (Hirschfelder and Kirsten 1991) found increased glenoid retroversion in both the symptomatic and unsymptomatic shoulders of individuals with posterior instability; Grasshoff et al (Grasshoff et al 1991) found increased anteversion in shoulders with recurrent anterior instability.
Changes in version may be difficult to quantitate on axillary radiographs unless the view is carefully standardized. Even with optimal radiographic technique the important contributions of the cartilage and labrum to the depth and orientation of the fossa (Howell and Galinat 1989; Soslowsky et al 1992) cannot be seen on plain radiographs or CT scans. When it is important to know the orientation of the cartilaginous joint surface in relation to the scapular body a double contrast CT scan is necessary.
A special feature of the glenohumeral joint is that the glenoid can be positioned on the thorax (in contrast to the fixed acetabulum of the hip).
Scapular alignment
This scapular alignment greatly increases the range of positions in which the criteria for glenohumeral stability can be met (see figure 26). Consider the arm elevated 90 degrees in the sagittal thoracic plane. This position can be achieved with the scapula protracted or retracted. If the scapula is protracted the humerus is closely aligned with the glenoid center line. When the humerus is in this position most of the humeroscapular muscles are oriented to compress the humeral head into the glenoid fossa. Alternatively if the scapula is maximally retracted the humerus is almost at right angles to the glenoid center line. In this position the net humeral joint reaction force is directed posteriorly and may not be contained within the balance stability angle. (Bradley and Tibone 1991; Glousman et al 1988; Inman et al 1994; Ozaki 1989; Poppen and Walker 1978; Warner et al 1992)
Which humeroscapular position is used to achieve a given humerothoracic position is a question of habit and training. The coordination of scapular position and glenohumeral muscle balance are important elements of the neuromuscular control of glenohumeral stability.
Atwater (Atwater 1980) has documented that in most throwing and striking skills the shoulder abduction angle is usually 100 degrees. Higher and lower release points are achieved by tilting the trunk rather than by increasing or decreasing the shoulder abduction angle relative to the trunk.
Properties of ligaments
Each glenohumeral ligament has clinically important properties which can be characterized by the relationship of the distance between its origin and insertion and its tension. (Frank 1996) These properties include:
- Its resting length (how far can its origin and insertion be separated with minimal force)
- Its elastic deformability (how much additional separation of the origin and insertion can be achieved by the application of larger forces without permanently changing the ligament's properties) and
- Its plastic deformability (beyond the ligament's elastic limit how much additional separation between the origin and insertion can be achieved by the application of larger forces which permanently deform the ligament up to the point where the ligament fails).
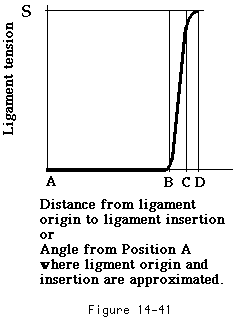
These properties can be demonstrated as a plot of the ligament's tension versus the distance between the ligament's origin and insertion. The same relationship pertains whether the ligament's origin and insertion are separated by translation of the humeral head or by rotation (see figure 27).
At point "A" the origin and insertion of the ligament are closely approximated. At point "B" the origin and insertion have been separated enough to initiate tension in the ligament. Thus the resting length of the ligament is shown as A-B. Stefko et al (Stefko et al 1995) measured the length of the anterior band of the IGHL to be 37 millimeters.
Additional separation of the origin and insertion causes increasing ligament tension. Up to point "C" this separation is elastic (i.e. it does not result in permanent change in the ligament). Further separation of the origin and insertion plastically deform the ligament up to the point "D" where the ligament fails at a tension of "S". The midsubstance strain to failure has been measured from 7 per cent - 11 per cent. (Stefko et al 1995)
Such graphs are helpful in describing the properties of ligaments:
The strength of a ligament is the amount of tension it can take before failure (S).
The laxity of a ligament is the amount of translation (see figure 28) or rotation (see figure 29) it allows from a specified starting position when a small load is applied. Ligaments with long A-B distances demonstrate substantial laxity if the starting point for laxity testing is close to "A." Laxity is diminished when the joint is positioned near the extremes of motion; that is when the starting point for the axity measurement is close to "B" (see figure 27).
Ligaments with small A-B distances are short or contracted.
Translational and rotational laxity are equivalent: they both reflect the ability to separate the attachment points of the ligament.
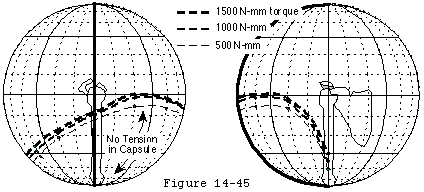
A typical relationship between humeroscapular position and torque (capsular tension X humeral head radius) is shown in figure 30. (Matsen Lippitt Sidles et al 1994) Note that the greatest part of glenohumeral motion and function takes place in the area where there is no tension in the capsule (corresponds to zone A-B in figure 27). Also note that at the limits of motion (corresponds to zone B-C) the torque increases rapidly with changes in position as suggested by the rapid increase in tension shown in figure 27.
These diagrams help distinguish laxity from instability. Normally stable shoulders may demonstrate substantial laxity; consider the very lax but very stable glenohumeral joints of gymnasts. In a most important study Emery and Mullaji (Emery and Mullaji 1991) found that of 150 asymptomatic shoulders in school children 50 per cent demonstrated positive signs of "increased laxity".
Some investigators have measured increased laxity in patients with glenohumeral instability. (Cofield et al 1993; Jerosch et al 1991; Jerosch et al 1991; Jorgensen and Bak 1995; Marquardt and Jerosch 1991) However recent evidence indicates that these differences are not always significant. (Harryman et al 1992; Lippitt et al 1994; Matsen Lippitt Sidles et al 1994) Starting in a neutral position the translational laxities of eight normal living subjects were found to be 8 ± 4 8 ± 6 and 11 ± 4 mm in the anterior posterior and inferior directions respectively. Interestingly virtually identical laxities were measured in sixteen patients requiring surgery because of symptomatic recurrent instability (see figure 31) indicating that in these subjects the measured laxity was not the determinant of glenohumeral stability. (Lippitt Harris Harryman et al 1994; Matsen Lippitt Sidles et al 1994) Sperber and Wredmark (Sperber and Wredmark 1994) found no differences in joint volume or capsular elasticity between healthy and unstable shoulders. These results indicate the amount of laxity cannot be used to distinguish clinically stable shoulders from those which are unstable.
The stretchiness of a ligament is its elasticity. Ligaments with long B-C distances (see figure 27) are stretchy and have "soft" end points on clinical laxity tests. Ligaments with short B-C distances are stiff and have "firm" endpoints on clinical laxity tests.
Biochemical composition (as in Ehlers Danlos) anatomical variation (anomalies of attachment) use (or disuse) age disease (e.g. diabetes frozen shoulder) injury and surgery (e.g. capsulorrhaphy) can affect the strength laxity and stretchiness of glenohumeral ligaments.
Ligamentous stabilization
The glenohumeral ligaments exert two stabilizing effects:
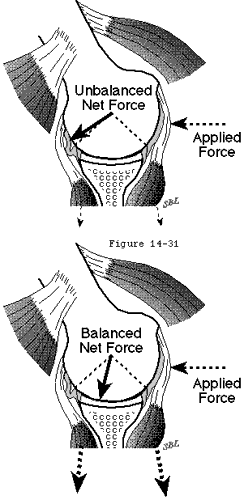
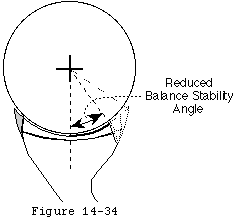
They serve as check reins restricting the range of joint positions to those which can be stabilized by muscle balance. This is important because at extreme glenohumeral positions the net humeral joint reaction force becomes increasingly difficult to balance within the glenoid (see figure 32). For example excessive abduction extension and external rotation of the shoulder may allow the net humeral joint reaction force to exceed the anterior-inferior balance stability angle. Similarly excessive posterior capsular laxity allows the net humeral joint reaction force to achieve large angles with the glenoid center line angles which may exceed the posterior balance stabilityangle. Furthermore at the extremes of motion the muscles tend to be near their maximal extension a position in which their force-generating capacity is diminished. (Lieber 1992)
The patient can modify the check rein function by altering the position of the scapula (see figure 33). Surgeons can modify the check rein function: capsular tightening moves points B C and D closer to point A reducing laxity (see figure 27). The check rein function is inoperant when the ligament is not under tension (i.e. when the humeroscapular position is within the tension free zone (A-B in figure 27 see also figure 30).
When torque is applied to the humerus so that a ligament come under tension this ligament applies a force to the proximal humerus. Because of the attachments of the ligament this countervailing force both compresses the humeral head into the glenoid fossa and also resists displacement in the direction of the tight ligament (see figure 34).
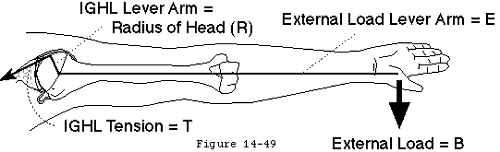
An analysis of ligament function (footnote 1) demonstrates the limits of the stability provided by ligaments acting alone. For example it suggests that if the torque resulting from a force of a modest 10 pounds applied to the arm at a distance of 40 inches from the center of a humeral head with a one inch radius was resisted only by the tension in the inferior glenohumeral ligament (IGHL) the IGHL would need to be able to withstand a tension of 400 lbs (see figure 34).
If tension in the ligament exceeds the strength of the ligament (S) the ligament breaks. A few investigations have attempted to measure the strength of the glenohumeral capsular ligaments. Kaltsas (Kaltsas 1983) has studied some of the material properties of the shoulder capsule and found it to be more elastic and stronger than the capsule of the elbow. He noted that the entire glenohumeral capsule ruptured at 2000 Newtons of distraction (450 lbs). Stefko et al (Stefko et al 1995) found the average load to failure of the entire IGHL to be 713 N or 160 lbs. Bigliani et al (Bigliani et al 1992) noted in sixteen cadaver shoulders that the IGHL could be divided into three anatomical regions: a superior band an anterior axillary pouch and a posterior axillary pouch of which the thickest was the superior band (2.8 mm). With relatively low strain rates the stress at failure was found to be nearly identical for the three regions of the ligament averaging 5.5 MPa which is 5.5 Newtons (1.2 lbs) per square millimeter. Thus to function as the primary stabilizer for a load of 300 lbs as in the example above the IGHL's of these cadavers would need to be 250 square millimeters in cross section. Thus no experimental measurements have demonstrated that the IGHL alone is sufficiently strong to balance the torque resulting from a load of 10 pounds applied to the arm at a distance of 30 inches from the center of a humeral head.
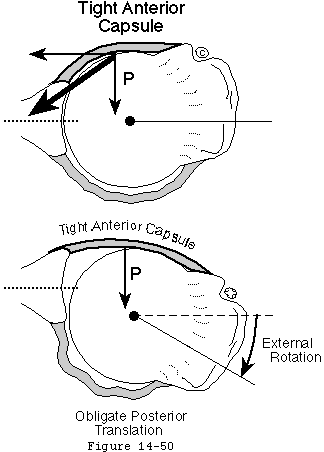
Excessive ligament tension can produce obligate translation of the humeral head. Harryman et al (Harryman Sidles Clark et al 1990) demonstrated that certain passive motions of the glenohumeral joint forced translation of the humeral head away from the center of the joint. This obligate translation occurs when the displacing force generated by ligament tension (quantity "P" in figure 34) overwhelms the concavity compression stability mechanism (see figure 36).
In Harryman's study anterior humeral translation occurred at the extremes of flexion and cross body adduction while posterior humeral translation occurred at the extremes of extension and external rotation. Operative tightening of the posterior portion of the capsule increased the anterior translation on flexion and cross-body adduction and caused it to occur earlier in the arc of motion compared with the intact joint. Operative tightening of the posterior part of the capsule also resulted in significant superior translation with flexion of the glenohumeral joint. These data indicate that glenohumeral translation may occur in sports when the joint is forced to the extremes of its motion such as at the transition between late cocking and early acceleration. Such obligate translations may account for the posterior labral tears and calcifications seen at the posterior glenoid in throwers. In addition these results point to the hazard of overtightening the glenohumeral capsule which may result in a form of secondary osteoarthritis known as capsulorrhaphy arthropathy. Hawkins and Angelo (Hawkins and Angelo 1990b) pointed to these complications of obligate translation in overtightened capsular repairs.
Footnotes
Footnote 1: The magnitude of the countervailing force is determined by the applied torque and limited by the strength of the ligament. The direction of this force is tangent to the humeral head at the point of its contact with the glenoid rim.
The countervailing force mechanism operates in the arc B-C where the ligament is elastically deformed. If the ligament behaves perfectly elastically the tension in the ligament provides a stabilizing force (T) where:
T = (Angular position - angle B) diameter of humeral head Pi/360° * spring constant of the ligament.
This relationship predicts that until angle B is reached no force is generated by the ligament the larger the angle past position B the more force is generated (up to the elastic limit) stiffer ligaments generate more force for a given angular displacement and larger humeral heads generate more force for each degree of angular displacement.
Ligament tension results from applied torque. When an externally applied force B acts at a distance E from the center of the humeral head it creates a torque (Q) which is the product of B and E (see figure 9). If this torque is resisted by a ligament closely applied to the humeral head (i.e. the effective moment arm equals the head radius(R)) the tension in the ligament (T) is
T = Q/ R = B * E/R
It is apparent that the relaxed glenohumeral joint is held together without either active muscle contraction or ligament tension.
Resting stability
It is apparent that the relaxed glenohumeral joint is held together without either active muscle contraction or ligament tension. The intact shoulder of a fresh anatomical specimen (Kumar and Balasubramaniam 1985a) the anesthetized and paralyzed shoulder of a patient in the operating room and the arm relaxed at the side (Basmajian and Bazant 1959) all maintain the normal relationships of the glenoid and humeral joint surfaces. This resting stability is due to a group of mechanisms including adhesion/cohesion the glenoid suction cup and limited joint volume. These mechanisms save energy as was pointed out by Humphry in 1858 (Humphry 1858): "We have only to remember that this power is in continual operation to appreciate the amount of animal force that is economized."
This is a stabilizing mechanism by which joint surfaces wet with joint fluid are held together by the molecular attraction of the fluid to itself and to the joint surfaces.
Cohesion and adhesion
Fluids such as water and joint fluid demonstrate the property of cohesion; that is they tend to stick together. Some surfaces such as clean glass or articular cartilage can be wet with water or synovial fluid meaning that the fluid adheres to them. When two surfaces with adherent fluid are brought in contact the adhesion of the fluid to the surfaces and the cohesion of the fluids tend to hold the two surfaces together (like two wetted microscope slides). The amount of stability generated by adhesion-cohesion is related to the adhesive and cohesive properties of the joint fluid the "wetability" of the joint surfaces and the area of contact between the glenoid socket and the humerus. Joint fluid has the highly desirable properties of
- having high tensile strength (difficult to pull apart) and
- having little shear strength (allows easy sliding of the two joint surfaces on each other with low resistance). (Simkin 1988)
The adhesion/cohesion effect is reduced by any factor that lowers the cohesion of joint fluid (such as in inflammatory joint disease) reduces wetability of the joint surfaces (as may occur in degenerative joint disease) or diminishes the glenohumeral contact area (such as in a displaced articular surface fracture or a congenitally small glenoid). It is also noteworthy that adhesion/cohesion forces do not stabilize a prosthetic shoulder replacement because metal and polyethylene are insufficiently compliant to provide the necessary near-perfect congruence and because water does not adhere to their surfaces.
Suction
This mechanism provides stability by virtue of the seal of the labrum and capsule to the humeral head (see figure 37). A suction cup adheres to a smooth surface by expressing the interposed air or fluid and then forming a seal to the surface. A rubber suction cup is noncompliant in the center but becomes more flexible toward its periphery. In a similar manner the center of the glenoid is covered with a relatively thin layer of articular cartilage. At greater distances from the center the articular cartilage becomes thicker providing greater flexibility. More peripherally the glenoid labrum and finally the capsule provide even more flexibility. This graduated flexibility permits the socket to conform and seal to the smooth humeral articular surface. Compression of the head into the glenoid fossa expels any intervening fluid so that a "suction" is produced that resists distraction.
The glenoid suction cup stabilization mechanism was demonstrated by Harryman et al. (Harryman Lazarus Sidles et al 1996) In elderly cadaver shoulders without degenerative changes the suction cup resisted an average of 20 ± 3 Newtons of lateral traction (about four pounds). Creating a defect in the labrum completely eliminated the suction cup effect. No suction cup effect could be demonstrated in the two shoulders with mild degenerative change of the joint surface. It is likely that this effect would be even stronger in younger living shoulders in which the articular cartilage glenoid labrum and joint capsule are larger more hydrated and more compliant. Like stabilization from adhesion-cohesion the glenoid suction cup centers the head of the humerus in the glenoid without muscle action and is effective in midrange positions in which the capsule and ligaments are not under tension.
Relative vacuum
This is a stabilizing mechanism in which the humeral head is held to the glenoid by the relative vacuum created when they are distracted (see figures 38 and 39). While it is common to speak of the glenohumeral joint space there is essentially no space and minimal free fluid within the confines of the articular surfaces and the joint capsule of the normal glenohumeral joint. The scarcity of fluid within the joint can be confirmed on MRI scans of normal joints on inspection of normal joints and on attempts to aspirate fluid from normal joints. The appearance of the potential joint volume can only be demonstrated after instilling fluids such as air saline or contrast materials into the joint. Osmotic action by the synovium removes free fluid keeping a slightly negative pressure within the normal joint. (Levick 1983; Müller 1929; Simkin 1988) This negative intra-articular pressure holds the joint together with a force proportional to the joint surface area and the magnitude of the negative intra-articular pressure. For example if the colloid osmotic pressure of normal synovial fluid is 10 mm Hg and the colloid osmotic pressure of the synovial interstitium is 14 mm Hg the equilibrium pressure in the joint fluid will be -4 mm Hg. (Simkin 1988) This negative intra-articular pressure adds a small amount of resistance to distraction (about one ounce per square inch) to the limited joint volume effect. Because the normal joint is sealed attempted distraction of the joint surfaces lowers the intra-articular pressure even more progressively adding substantial resistance to greater displacement. (Harryman Lazarus Sidles et al 1996; Itoi et al 1993)
The limited joint volume effect is reduced if the joint is vented (opened to the atmosphere) or when the capsular boundaries of the joint are very compliant. Under the latter circumstances attempted distraction draws the flexible capsule into the joint producing a "sulcus" (see figures 38 and 39). The decreased stability from venting the joint was initially described by Humphry in 1858(Humphry 1858) and subsequently by others. (Cotton 1921; Fairbank 1948; Kumar and Balasubramaniam 1985b; Neer 1970; Ovesen and Nielsen 1985a; Ovesen and Nielsen 1985b; Sidles et al 1989; Thompson and Winant 1950; Thompson and Winant 1961; Wulker Rossig Korell et al 1995) Gibb et al (Gibb et al 1991; Matsen Lippitt Sidles et al 1994) found that simply venting the capsule with an 18 gauge needle reduced the force necessary to translate the head of the humerus halfway to the edge of the glenoid by an average of 50 percent. Wulker(Wulker et al 1993) found that venting the joint increased the joint displacement with an applied load of 50 N by 50 per cent in all directions.
From these results it is expected that glenohumeral stability from limited joint volume is compromised by arthrography arthroscopy articular effusions hemarthrosis and in other situations in which free fluid is allowed to enter the glenohumeral joint. In a very interesting study Habermeyer et al (Habermeyer and Schuller 1990; Habermeyer et al 1992) found the mean stabilizing force obtained by atmospheric pressure was 146 N (32 lbs). In fifteen stable living shoulders traction on the arm caused negative intra-articular pressure proportionate to the amount of force exerted. In contrast unstable shoulder joints with a Bankart lesion did not exhibit this phenomenon.
These stabilizing mechanisms may be overwhelmed by the application of traction as in the cracking of the metacarpophalangeal joint. A "crack" is produced as the joint cavitates: subatmospheric pressure within the joint releases gas (>80 per cent carbon dioxide) from solution in the joint fluid. This is accompanied by a sudden increase in the separation of the joint surfaces. Once a joint has cracked it cannot be cracked again until about 20 minutes later when all the gas has been reabsorbed. (Roston and Haines 1947; Unsworth et al 1971)
Superior stability benefits from all the same mechanisms as anterior posterior and inferior stability: glenoid orientation muscle balance glenoid shape ligamentous effects adhesion/cohesion the suction cup and limited joint volume.
Centering and stabilization
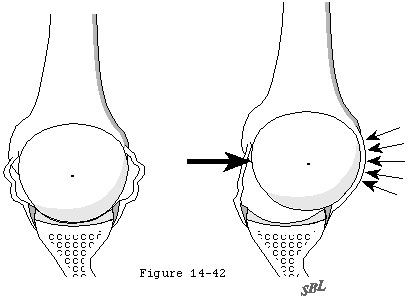
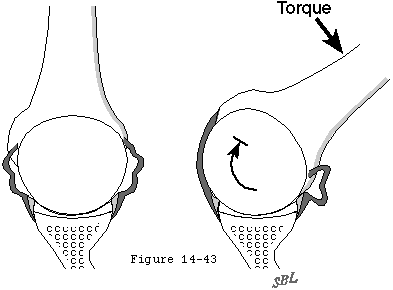
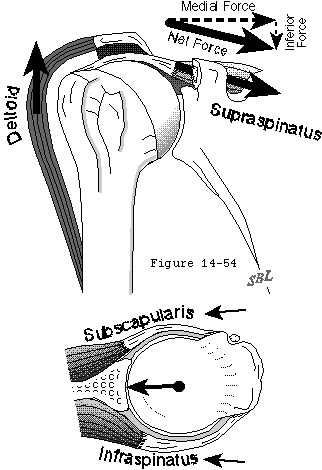
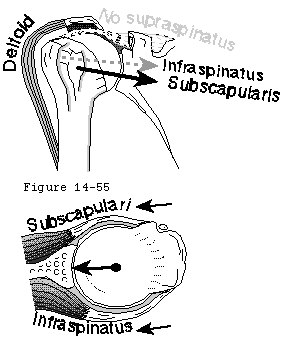
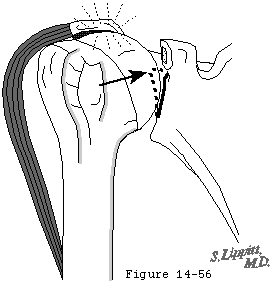
Compression of the humeral head into the glenoid concavity is an important mechanism by which the head of the humerus is centered and stabilized in the glenoid fossa to resist superiorly directed loads (see figure 40). Even when a substantial supraspinatus defect is present compression from the subscapularis and infraspinatus can hold the humeral head centered in the glenoid (see figure 41). More severe cases of chronic rotator cuff deficiency however may be associated with superior subluxation of the head of the humerus and wear on the superior lip of the glenoid fossa (see figure 42). This erosive wear flattens the superior glenoid concavity and thereby reduces the effective glenoid depth in that direction. Once the effective superior glenoid depth is lost repair of the rotator cuff tendons or complex capsular reconstructions cannot completely restore the glenohumeral stability previously provided by concavity compression (see figure 43).
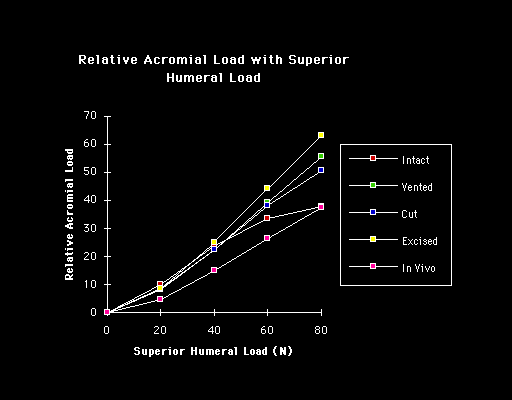
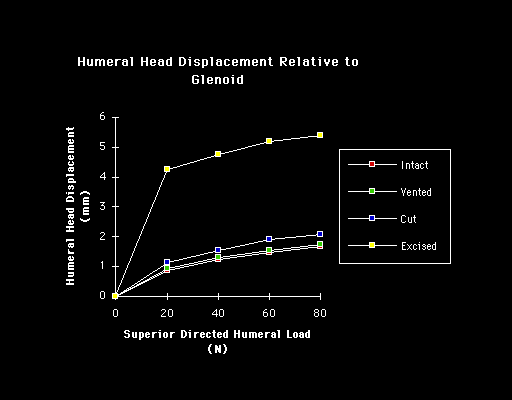
In addition to the mechanisms which stabilize the shoulder in other directions there is a unique aspect of superior stability: the ceiling effect provided by the superior cuff tendon interposed between the humeral head and the coracoacromial arch. As every shoulder surgeon has observed in the normal shoulder in a resting position there is no gap between the humeral head the superior cuff tendon and the coracoacromial arch. As a result the slightest amount of superior translation compresses the cuff tendon between the humeral and the arch. Thus when the humeral head is pressed upwards (for example when pushing up from an arm chair or with isometric contraction of the deltoid) further superior displacement is opposed by a downward force exerted by the coracoacromial arch through the cuff tendon to the humeral head. Ziegler et al (Ziegler et al 1996) demonstrated this stabilizing effect in cadavers by demonstrating acromial deformation when the neutrally positioned humerus was loaded in a superior direction. By attaching strain gauges percutaneously to the acromion they were able to measure its deformation under load. The acromion thus became an in situ load transducer. By applying known loads to the acromion they were able to derive calibration load-deformation curves which were essentially linear. Superiorly directed loads applied to the humerus were then correlated with resulting acromial loads and with superior humeral displacement. In ten fresh cadaver specimens with the superior cuff tendon intact but not under tension superiorly directed loads of 80N produced only 1.7 mm of superior displacement of the humeral head relative to the acromion. When the cuff tendon was excised a similar load produced a superior displacement of 5.4 mm. (p < .0001). In specimens where the cuff tendon was intact an upward load of 20 N gave rise to an estimated acromial load of 8 N. Greater humeral loads up to 80 N were associated with a linear increase in acromial load up to 55 N when an upward load of 80 N was applied (see figure 43). In a single in vivo experiment where the acromion was instrumented and calibrated as in the cadavers very similar relationships between upward humeral load and acromial load were noted (see figure 43). These acromial loads must have been transmitted through the intact cuff tendon. When the tendon was excised the humeral head rose until it contacted and again loaded the acromial undersurface (see figure 44).
Flatow et al (AAOS 1996) (Flatow et al 1996) used a cadaver model to explore the active and passive restraints to superior humeral translation. Whereas Ziegler's study was conducted with the arm in a neutral position with axial loads Flatow's involved abducting the humerus with simulated deltoid and cuff muscle forces. Both groups noted that the presence of the supraspinatus tendon limited superior translation of the humeral head even if there was no tension from simulated muscle action.
Both Ziegler and Flatow cautioned that the effectiveness of the cuff tendon as a superior stabilizing mechanism is dependent on an intact coracoacromial arch. Sacrifice of the ceiling of the joint the coracoacromial ligament or the undersurface of the acromion can be expected to compromise the resistance to superior displacement of the humeral head.
127